UNIVERSITY OF BELGRADE
FACULTY OF MINING AND GEOLOGY
đuina 7, Belgrade, Republic of Serbia
TECHNICAL RESULT m85
Software solution for coal quality control at the mine planning
phase
Softver za upravljanje kvalitetom
uglja u fazi planiranja eksploatacije uglja
Project
Name:
IMPROVEMENT OF LIGNITE OPENCAST MINING TECHNOLOGY IN
ORDER TO INCREASE ENERGY EFFICIENCY AND OCCUPATIONAL SAFETY
UNAPREĐENJE
TEHNOLOGIJE POVRINSKE EKSPLOATACIJE LIGNITA U CILJU POVEĆANJA ENERGETSKE
EFIKASNOSTI, SIGURNOSTI I ZATITE NA RADU
TR 33039
November 2013
Type of technical solution |
M85 - Software
development |
|
Authors |
Kolonja B.,
Kneević D., Lilić N., Stanković R. Stevanović D.,
Kolonja Lj., Banković M., Tomaević A. |
|
Name of technical solution |
Software solution for
coal quality control at the mine
planning phase |
|
To whom is a technical solution intended |
Electric Power Industry of Serbia |
|
The user of the technical solution |
MB "Kolubara", OPM "Kostolac" |
|
The year
of development |
2012/2013 |
|
Verification
of results |
By reviewers:
|
|
The
technical solution accepted by |
Faculty of Mining and Geology University of Belgrade |
|
Application
of results |
Electric Power Industry of Serbia |
|
Vrsta tehničkog reenja |
M85 Razvoj
softvera |
|
Autori tehničkog reenja |
Kolonja B.,
Kneević D., Lilić N., Stanković R. Stevanović D.,
Kolonja Lj., Banković M., Tomaević A. |
|
Naziv tehničkog reenja |
Softver za upravljanje kvalitetom uglja u procesu
planiranja eksploatacije uglja |
|
Za koga je raneno tehničko reenje |
Elektroprivreda Srbije |
|
Ko koristi tehničko reenje |
PD RB Kolubara, TE-KO Kostolac |
|
Godina izrade tehničkog reenja |
2012/2013 |
|
Verifikacija rezultata |
Recenzenti:
|
|
Ko je prihvatio tehničko reenje |
Rudarsko-geoloki
fakultet Univerzitet
u Beogradu |
|
Primena rezultata |
Elektroprivreda Srbije |
Software solution for coal quality control at the
mine
planning phase
1.
Technology field of the technical result
The technical result is a software solution for
coal quality control
at the mine
planning phase and
belongs to the field of Energy, Mining Industry
and Energy Efficiency.
2.
Technical problem - Coal quality control at the mine
planning phase
Mine
planning is based on reliable estimates of coal grades of future mining blocks.
Consequently, in order to develop any coal quality control strategy, the mine
should have the capability to predict both the quality and the variability of
the pertinent coal parameters with some degree of certainty. Coal quality
cannot be controlled without some information about possible qualities of
future mining blocks. The control of coal quality at the mine phase is usually
planned from in-situ coal parameters which are estimated from coal samples.
These samples are commonly used to generate maps of in-situ coal parameters.
With such maps, it is possible to know in advance the effect of mining from
different benches of the surface mine, i.e., whether or not the required
quantity and quality of coal can be met during the planning period. Mine planning
is divided into four categories: long-term, medium-term, short-term and
operational planning [10].
The primary objective of long-term mine
planning is to develop mining sequences which will define the economic limit of
the mine. Because planning is usually done with relatively scanty information,
an effective coal quality (coal grade) control is not practically possible. The
medium-term planning is concerned with a time span from one to about ten years.
It provides information necessary for forecasting future production and cost.
There is also practical limitation in controlling coal quality during this
planning, owing to limited information about grades. The short-term planning
contains all activities which are planned between one and twelve months period.
The short range plan defines resources and labor requirements, future
production and cost. More distinct information about the nature of
mineralization and equipment performance is required in short range than medium
range planning.
Operational planning is concerned with daily or weekly
requirements of the mine. Proper operational planning must conform to short
term mine plans as well as satisfying many practical details that are unique to
day to day operations. Grade control problems are usually incorporated in the
operational planning provided that the necessary detail information is known in
advance. The planning objective may vary between mines. However, the most
common planning objective is maximization of tonnage, while meeting the
requirements of physical and geological constraints, policies and mining
methods. The basic data required in any operational planning are grade(s) or
coal quality and capacity. Difficulties in optimum production schedule are
caused by variability of grade and inability to accurately predict grades of
smaller mining units. Therefore, detailed information on coal properties is
essential for reliable operational mine planning [11].
Generally two
types of grade variability exist in the coal chemical composition (Fig.1):
Long-term variability as measured
by trends of monthly or longer duration.
Operational variability is
generally measured by short period inter-train variability around the long-term
trend and is little affected by the long-term variability.
The
objectives of the operational mine planning model considered in this study are
two-fold. First, the coal quality requirements for a planning period must be
met, subject to some physical and geological constraints, policies and mining
methods. Secondly, the quantity requirements must ensure sufficient coal production.
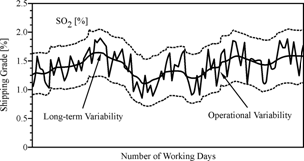
Figure 1: Long-term and operational variability of SO2 grade
This model, in
general, is based on predicted information about the in-situ quality of the
coal deposit. Consequently, production scheduling for the purpose of
controlling coal quality, e.g., sulfur, have to be based on the predicted data
of the contemplated mining benches. The model uses zero-one programming formulation to
select potential working benches in surface coal mine on the basis of predicted
information. The standard optimization technique widely used in many
industrial applications is the linear and integer programming [12]. Models involve optimization of a quantity usually
referred to as the objective function subject to a set of constraints which
define the feasibility. In the operational mine scheduling, the decision to be
made is which working benches should be mined. A decision variable (1)
represents the i-th working bench and takes on a value of either zero (0) or
one 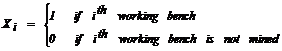(1).
(1)
With Xi denoting the i-th
working coal bench whose predicted sulfur and tonnage values for a planned
period, are sulfur (Si,%) and coal production (Ti, tons),
respectively, the objective function of an integer programming formulation of
reducing total sulfur content is expressed by equation (2) below.
, where n is the total number of coal working
benches. (2)
The restriction with
regard to both quality and tonnage requirements are formulated in the following
way. First, run of mine composite sulfur (3) must not exceed maximum allowed, Smax (%), during a shift (or period).
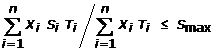(3)
Also, all working bucket wheel excavators (BWE's) must mine coal during a
period (or shift). This constraint (4) which guarantees a minimum production
during a period, assumes that during any period, the available BWE's do not
exceed the total number of potential working coal benches.
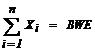(4)
In practice, the surface coal mine is divided
into a number of mining phases, which are mined bench by bench, each bench
represented by a horisontal layer of blocks within the given mining phase and
having the same elevation. The mathematical formulation of the scheduling
procedure of mining blocs in terms of binary decision variables describing in
which period the particular block is extracted and what is its destination
(either directly to the power plant or to processing plant and stockyard) is
quite straightforward. But the hypothetical optimal block extraction sequence
may be completely impractical due to the technological requirements for the
mining equipment (BWE's) access and relocation.
3.
General research overview
According
to the International Energy Agency [1] forecast
for the next decades, coal will retain its important role in power generation
in Europe and worldwide. The availability of the worldwide coal resources and
their price stability are the main reasons for this trend. Coal is the most
important fuel in the generation of electricity, accounting for 65% of the
power produced in Serbia [2]. In the
past, because of the regulated business environment in which utilities
operated, coal was viewed as a necessary evil and was always treated as a
"pass through" cost. Although the quality of coal impacts boiler
operations and subsequent power produced and emissions, utilities had no
economic interest in monitoring or managing coal quality.
It is preferred that feeds the plants coals whose
properties, especially that of calorific value, conform to the power plant
design and whose sulfur content meets the sulfur emission requirement after
combustion. It is generally difficult to obtain coal of desired qualities from
one source because of the variable nature of coal properties. Homogenization of
coals from different working benches within the single mine or even more mines
are therefore becoming mandatory not only from an economic standpoint but also
from the necessity of meeting emission requirements.
At
the surface mine, coal is extracted from various active working benches and
then transported directly to the power plants or to stockyards. Because coal
properties can vary considerably, the quality of run of mine (ROM) coal
composite will depend on both the quality and quantity of coal mined from each
active bench. If it is desired to control the ROM coal quality, the rate of
coal production from each active bucket wheel excavator (BWE) should be
regulated. The effect of this approach is to blend the coal through the
sequence of mining. Such an approach requires a prior knowledge of the coal
quality of planned mining blocks.
Coal homogenization is one of mostly used options for
optimisation of sulfur emissions from desulfurazation power plants [2]. However, decisions about coal homogenization must
deal with uncertainty and variability in coal properties, and with the effect
of off-design coal characteristics on power plant performance and cost. According to Shih and Frey [3] sulfur and ash content and heating value are
considered as normally distributed random variables. The objectives of a model
to optimize operation of a plant must include minimizing: (i) the expected
(mean) costs of coal blending; and (ii) the variance of coal blending costs.
The cost objective function includes coal purchasing cost, ash disposal cost,
sulfur removal cost, and fuel switching costs. Chance constraints include
several risk measures, such as the probability of exceeding the sulfur emission
standard.
Homogenization piles are frequently used in order to
reduce variability and ensure coal stock. In this context, the most important
factors, in respect to pile building can be cited as the type of layer
disposition, number of layers and added mass. The last variable can
significantly reduce pile variability when a large material amount is
homogenized, and variability among the lots decreases [4, 5]. The deposition sequence of the material also is able
to affect grade predictability of each pile, requiring a more careful mining
advance forecast. Often, this scheduling is represented by a vector of grades
to coal blocks that will be mined along a given activity time, and
geostatistical techniques are used to predict them.
Some
previous studies involving blending and homogenization piles and geostatistical
simulations are described [6, 7]. US power stations have experienced reduction in SOx
emissions, by up to 20%, by homogenizing coal feeds to power plants [11].
Kriging technique is a very good estimator, but it is
not adequate to predict the uncertainty of a process. According to [9], on contrary to kriging, geostatistical simulation
methods aim to reproduce in situ variability,
and the spatial continuity of the input data set. Models used in this way, aim
to replicate the spatial structure of a data set as a whole rather than provide
reliable local estimates of an attribute at particular locations.
The stochastic simulated model honors values at the
sampled points and it reproduces the same dispersion characteristics of the
original data set (i.e. the mean, variance and covariance or variogram). It is
possible to address questions referring to the dispersion of the grades during
operational mine planning or stocking process, since the dispersion
characteristics of the original data are maintained.
4.
Description of the technical solution
4.1. Coal
homogenization at the stockyard phase
Homogenization is stocking the ROM coal in
layers, in their correct proportions, in the same stockpile, then reclaiming
across the full face. In any blending pile the attenuation on variability
depends on the equipment used and the way coal is stocked and reclaimed [6].
The main factors influencing
blending efficiency are the pile size or its mass and the number of layers used
to build pile. The aim in the homogenization process is to narrow down the
standard deviation of the normal distribution. A measure of the quality of the homogenizing process
is defined by the homogenizing efficiency (HE). In
simplified terms, and subject to certain statistical assumptions, the resultant
homogenizing effect is
calculated as the variability of the incoming coal on
pile (e.g. S %) and the variability of the outgoing coal from pile [13]:
@ 0.5 
, where n is
number of layers. (5)
By
grouping exploitation mining blocks and forming a pile, the average grade of
this pile is closer to the planned mean if compared to the grades of each
individual block which comprise the pile. This phenomenon of variance reduction
is well known and it is referred to as the volume-variance relationship [4, 5].
Prior to designing the homogenization stockyard it is necessary to
know the sulfur content of coal that will form the pile. These grades come from
a geological block model mined according to a sequence determined by an optimal
mine scheduling. These block models however are obtained via classical
interpolation algorithms, such as ordinary kriging. In these situations, the
uncertainty associated with the interpolated value cannot be properly
incorporated [9]. As a
result of the so-called smoothing effect, the variance of the estimated values
is smaller than that of the original data. There are also limitations
associated with the use of the kriging variance as a measure of uncertainty [8].
The methodology suggested in this study quantifies the variability
of the homogenization pile by using multiple equally probable realizations
derived from a lognormally simulated sulfur distribution. Models used in this
way, aim to replicate the spatial structure of a data set as a whole rather
than provide reliable local estimates of an attribute at particular locations.
4.2. The stocking model
From
operational mine plan the coal benches mined are forming each windrow stockyard
pile. These multiple mining benches are an initial blending attempt as distinct
coals are combined to ensure sulfur regularity minimum.
Software
solution takes as input all needed design parameters, so very detailed analyses
are possible. First input parameter is number of layers in base, from which
software calculates total number of layers. There are n layers in the
base. One can observe that there is an n-1 layer in the next row, but
also that rhombus, and corner shaped layers are paired. So, in all non-base
rows of layers, there is
pairs of
square and corner shaped layers. Then total number of all base and non-base
rows is
(6)
So,
the total number of layers is the square of number of layers in base. So, for
example, if input number is 10, then total number of layers in pile is 100.
The stockpile geometry is given with: length, width, height and
slope are also input parameters. The software solution give possibility to
define stockpile geometry (shape) with length, width, height and slope as input
parameters, that provides easy adjustment for other, different stockpile size
and shape. Another feature of interface is visualization of cross section for
different stacking granularity, for selected pile and position within pile,
Figure 2. The shadings of layers cross sections in Figure 2 are corresponding
to the percentage of sulfur.
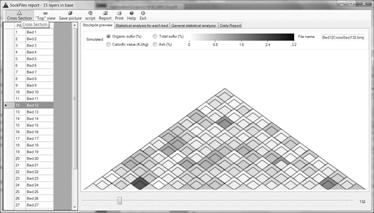
Figure 2. Software visualization of pile
cross section
4.3. The
reclaiming model
Developed reclaiming model determines the tonnage of
coal to be loaded from stockyard piles by reclaimer, so that the total sulfur
content of the reclaimed coal is minimised, while retaing the its heating value
within required range.
When a given pile is reclaimed at
the stockyard to feed the power plant, its real sulfur content is accessed via
averaging the sulfur contents from generated samples along time intervals. This
average sulfur content is the possible value to be used as real feeding values
for power plants.
Bed blending assumes that each reclaim slice (Fig. 3) includes
equal amounts of material from all layers of material stacked. This is good
approximation for some bed-blending systems, but it is not a good approximation
for most mineral stockpiling systems. Therefore, we describe prediction of the
performance of stockpiling systems for which reclaim slices include unequal
amounts of material from the layers of material stacked, Fig. 3.
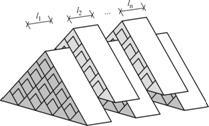
Figure 3. Reclaiming slices from windrow pile
Quality
of the reclaimed material is calculated as the weighted average of pieces of
the layers that are taken from the bed. In this calculation, each pieces
quality is weighted by its volume. More precisely, let 
be the average
grade of the material in layer 
such that its
distance from the beginning of the layer is in the range 
where 
the cut depth of the reclaimed is. Now, the layers can
be described by the matrix
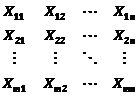
where 
is the number of
stocked layers, 
is the length of
the bed, and 
. The volume of the material reclaimed from layer 
in cut 
is denoted by
. The average grade of material reclaimed in whole cut is then computed
by the formula
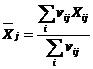. (7)
When necessary, calculation of volumes includes Monte
Carlo integration for calculation of intersection area of arbitrary polygons
when the polygons are too complex. We describe the Monte Carlo integration
method we used. Let 
be a function,
and 
the definite
integral of that function
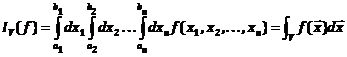(8)
on the
region of integration
. (9)
Monte
Carlo approximation of this definite integral is calculated using
(10)
where 
is the volume of
the integration region, and 
are the points
in the random sample taken from the integration region. The value 
converges to
true value as 
goes to
infinity. The variance of this estimate is calculated as
(11)
Since
the variation of an integral able function is bounded, the variance of the
estimate decreases as 
Now, let 
be the
characteristic function of the polygon
. For each point, this function gives value 1 if that
point is in the polygon and value 0 if the point is out of the polygon. This
function can be calculated by taking an arbitrary ray (half-line) from the
point that intersects the sides of the polygon. If the number of intersections
is even, then the value of the function is 0, and if it is odd, the value of
the function is 1. By plugging this function in the general formula for Monte
Carlo integration, one can approximate the area of the polygon. In order to calculate
the intersection of the polygons
, one should use the characteristic function of the
intersection which is the product of characteristic functions of polygons,
namely, 
Nevertheless, in
often, the volume can be calculated exactly without approximation.
4.4.
Simulation methodology of coal quality control
The
primary objective of the simulation is to determine a sequence of mining tasks
to deliver the required coal quality and quantity to the power plants in the
short-to-medium term.
Simulation algorithms currently used in mining is more
appropriate than ordinary kriging to deal with matters related to data
variability. Mine production plans, scheduling, and blending strategies require
knowledge of the dispersion of relevant geological attributes [11, 14]. Fluctuations in mining engineering and geochemical
attributes of interest are also relevant for mine design and production
scheduling. For example, mapping the probability of grades exceeding a limiting
threshold within different areas of a deposit can warn of possible fluctuations
in the grades, with direct implications on the scheduled mining plan.
Stochastic simulation model is used to generate multiple,
equally probable scenarios of the phenomenon; each scenario reproduces the
value of the sampled data, their spatial continuity, represented by lognormal
model, and the histogram of the distribution, replicating the natural
variability of the sulfur. These scenarios provide a set of possible values for
each mining block, which form a homogenization pile. So, we generate many
values for the average of blending piles studied as there are various possible
scenarios generated by the simulation algorithm used.
Generation of dataset
for this case study was performed in statistical package Rsim [15, 16], with rlnorm function
which can generate random numbers whose distribution is lognormal, with
arguments: the number of random numbers, the mean and standard deviation. The
following code was used:
ss_mean=0.465; ss_stdev=0.351; ss_meanlog
=
ss_sdlog =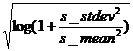 
; y = rlnorm(1, ss_meanlog, ss_sdlog)
The steps involved in the study can be
summarized as:
1.
Build a consistent geological
database using drill holes and use this data to develop MinexTM coal
quality seem models to map the variability associated with the in situ
qualities. The method used to estimate block sulfur
content for operating mining plan is gridding by inverse distance squared. Generation of multiple equally probable models via Rsim.
2.
After its
construction, a mini block model is used for mining planning and scheduling. For
a given mining schedule and multiple simulated quality models, compose the
average content values for each pile system considering the number of blocks
forming each chosen stockpile and their respective qualities. Each generated pile is based on a scheduled sequence
of blocks forming the pile.
3.
Plot the
standard deviation from stockyard pile qualities in relation to planned average
for various pile sizes (masses). Check the size of the pile, which leads to an
acceptable range of content variation. Repeat (2) and (3) for each of several simulated models
of sulfur contents to map the influence of in situ qualities uncertainty on the
interpile quality fluctuation.
5.
Case study
The case study uses data from a coal deposit
located in Kolubara surface mine, Figure 4. The operating mining plan uses for
grade estimation the original geological dataset. The local geology of mine
includes 3 coal seams interbedded with waste material such as siltstones,
sandstones, shales, and other sedimentary rocks. Available samples include 1118
heating values and 632 sulfur values for analysis distributed in the coal seams
mentioned above. The samples considered for this study were separated by coal
seams. Samples were collected and analyzed at different length or support as
each coal seam has thickness variations from point to point.
The
Kolubara surface mine used for simulation is bounded by a rectangle, and mine
sequencing is developed using the coal within the rectangle (Figure 4). The box cut is a planned start at the northern
extreme of the area due to several technical operational reasons including an
adequate location for the topsoil provisional deposit from the first cut. The
area to be mined over the life of the mine was divided into 28 strips, 200 m
wide. The deposit used to illustrate the
methodology has 3 mineable coal seams, each with its own coal quality and own
average thickness. To compose the sulfur grade value for a mining blocks, it is
necessary to combine multiple sulfur grade values from each different coal seam
and multiple working benches.
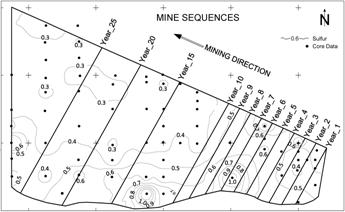
Figure 4.
Field to
be mined and the strip sequence by years
Analises
has shown that in Kolubara surface coal mine some parts of deposit with high
content of sulfur, over 2% (fig. 7). Adjusted on share of 95 percentiles
content of sulfur is over 1%, althought
content in the most of parts of the deposit is under 0.4%. The space
distribution of sulfur required the homogenization of coal according to sulfur
as a leading parametre. Slave parameter
for homogenization is coal heating value. The integral
model for coal quality control is developed and consists of three sub-models:
operational mine scheduling model, stocking model and reclaiming model, fig 5.
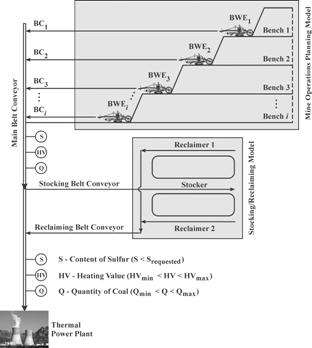
Figure 5. Technological scheme of coal
homogenization in Kolubara surface mine
According simulated daily or shift mine plan each BWE has working
bench position and production parameters. Mass and quality control will be done
by on-line devices and weightmeters on main belt conveyor. If coal quality has
required values coal is transported directly to thermal power plant, if not
coal is transported on stockyard. Stacking and reclaiming will be controled by
its models.
To proceed with the pile emulator, a mining sequence associated to
the mine plan is required. Mean of sulfur content at each stockyard pile
directly depends on the coal block extraction schedule. This sequence is
determined by a planned mine advance. Before starting the stocking and the
analysis on the variability reduction with the increase of the number of
stockyard pile layers, it is necessary to understand all variability sources
influencing the pile homogenization system of the case study, namely:
-
variability of the sulfur grades
from each coal seam and bench11, bench12,
benchij.
-
variability of the sulfur grades,
which feed the stockyard (pile combining coal from several mining benches or
mines)
-
variability
among grades in homogenization piles (variability depending on number of
layers).
In this study we use a pile of 350.000 t
equivalent to new designed stockyard at the mine corresponding to 84 mining
blocks from the model. Piles were designed as 48 m wide and same length according
to the variable number of layers. To illustrate the procedure, the blocks
selected corresponded to the first year of production with a total of 4895
blocks. Each block has a grade obtained by Rsim, which, of course, differs
among them and is different from the global mean calculated for the first year.
By grouping various blocks and forming a pile, the average grade of this pile
is closer to the global annual mean when compared to the grades of each
individual block which comprise the pile, Figure 6.
In this case study, we
analyzed the performance of the homogenization method for various blending bed
sizes. As illustration we present the variability of input and output data for
the cases of 25, 100 and 169 layers in each bed. Gray circles represent the
input data, horizontal axis corresponding to the cumulative mass of the coal
stacked up until the moment, and vertical axis corresponding to the percentage
of organic sulfur. Black circles represent the percentage of organic sulfur
after the homogenization. One can notice that the output consists of several
segments with rather small intersegment variation. Each segment corresponds to
one reclaiming cycle. The mean values of segments vary inevitably as the trend
changes in the input data.
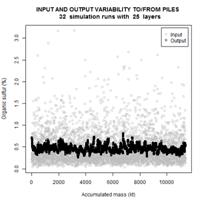
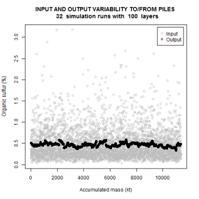
Figure 6. Simulation results for
input/output variability of sulfur on pile
This explains why the grades in the reclaimed
coal from the piles led to a variance reduction in the grades feeding the power
plants as compared to the grade variability that would be obtained from a
mining block by block scheme feeding the power plant. A few other aspects
controlling the variance of the average grades among stockpiles are:
-
the larger the size of stockpile the smaller will be the variance
of the average grade of each pile around the planned mean grade,
-
as a consequence of the stockpile
size an extremely large pile hypothetically perfectly homogenized formed by all
blocks mined during planned period would lead to a zero variance around the
mean grade of this period (in theory).
However, the larger the pile
the better will be the homogenizing process; and from an operational point of
wiew the problems tend to grow in difficultly as the size of the stockyard
equipment involved increases. The adequate pile size is the minimum size which
will deliver coal to the plant with grades varying within a pre-determined and
acceptable grade interval.
Given all information necessary from operational mine planning and
scheduling to the stockyard simulation model, i.e. simulated block values and
mining sequence, the average sulfur values of the homogenization piles can be
obtained. The variability among piles was determined for variable number of
layers in the same pile size. It was taken into consideration that the mass of
each mined coal block is equivalent to BWE capacity on each coal seam.
Figure 7.
shows that the simulated model adequately reproduced the histogram of the
declustered original data. Left part of the figure is plotted the histogram of
the original samples and in the right part the generated histogram by the
algorithm of sequential lognormal simulation for one geological domain studied.
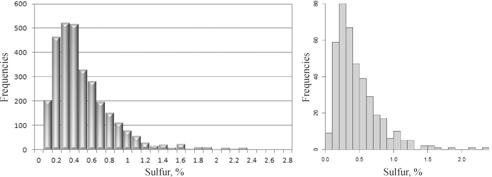
Figure 7. Histograms for sulfur original data (left) and (d) to
simulated values of sulfur (right)
Given the validated simulated block model and the planned
mining sequence, it is possible to calculate a set of equally probable values
for the sulfur average that each blending pile can take. A pile is formed by a
set of blocks from different mine faces from multiple benches. The scenarios generated
by sequential Gaussian simulation would provide a group of possible values to
the blocks that form a homogenization pile. Consequently, the average organic
sulfur content calculated for each pile can assume as many values as simulated
scenarios.
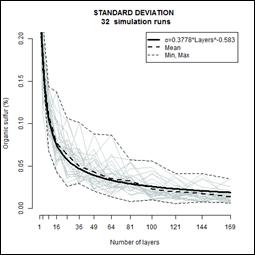
Figure 8. Average standard
deviation for variable pile sizes
The
algorithm developed considers the number of layers in piles and the
contribution that each seam from each block adds to the total mass of the pile.
When the number of layers and mass (size) of the pile is reached the algorithm
stops, takes the weighted average of the qualities from the blocks included in
this specific pile, and starts building the next pile.
Average
standard deviations for the sulfur from various pile sizes is given in Figure
8. The Figure illustrates the results
obtained for the intrapile standard deviation for each number of layers tested.
Note, the curves were plotted for all simulation runs constructing piles of
350.000 t and repeated 32 times (one for each simulated number of layers). It
is noticed that after 100 layers the standard deviation stabilizes. The curves
with the fitted (thick), minimum, average and maximum (dashed) standard
deviations versus the number of layers were highlighted. Horizontal axis refers
to the number of layers. Vertical axis refers to the standard deviation. An
exponential curve was fitted to these experimental points. The model derived
for the standard deviation of organic sulfur versus number of layers is shown.
6.
Conclusion
This technical solution reviewed
homogenization methods used in stockyards and proposed a methodology to
generate equally probable models mapping sulfur content within a coal deposit
in Kolubara surface mine. These models allow assessing the uncertainty
associated with the grade content in the ROM coal supplied to the power plant.
As the size (mass) of the pile increased, the quality fluctuations reduced
allowing the decision maker the choice of selecting a proper pile size to meet
an acceptable level of variability. The optimal size must be defined taking
into account capital and operational costs. The key message of stemming from the results in this
paper is that the simulation model provides a useful decision support tool to
compare operational mine scheduling and stockyard piles policies for controlling
coal quality. According to the model, it is possible to
reduce the variability of the grades exponentially as the mass of the pile
increases.
REFERENCES:
[1]
***, International energy outlook 2011, US Energy Information administration,
2011.
[2]
Ignjatović D., Kneević D., Kolonja B., Lilić N., Stanković
R.: Upravljanje kvalitetom uglja
("Coal quality management"), University of Belgrade, Faculty
of mining and geology, Belgrade, 2007.
[3]
Shih, J.S. and Frey, H.C. Coal blending optimization under uncertainty. Proceedings of the Tenth Annual
International Pittsburgh Coal Conference, Pittsburgh, Pennsylvania, 1993, pp.
11101115.
[4]
David, M., Developments in Geomathematics 2: Geostatistical ore reserve
estimation, First Edition.: Elsevier , Amsterdam 1977.
[5]
Parker, H. The Volume Variance Relationship: A Useful Tool for Mine Planning. Engineering and Mining Journal, vol. 180
(1979), pp.106123.
[6]
Schofield, C.G., Homogenisation/Blending Systems Design and Control for
Minerals Processing, TransTech Publications, Claustehall 1980.
[7]
***, A review of the state-of-the-art in coal blending for power generation,
Final Report - Project 3.16., CRC, 2001,
[8]
Isaaks, E.H. and Srivastava, R.M., Applied Geostatistics, Oxford University
Press, New York 1989.
[9] Costa, J. F.C. L., Marques, D., Pilger,
G.G., Koppe, J. C. , Ribeiro, D.T., Batiston, E.L. and Costa, M.S.A.,
Incorporating in situ grade variability into blending piles design using
geostistical simulation, Proceedings
of the 3rd World Conf. on Sampling and
Blending, Porto Alegre. vol. 1, 2007. pp. 378390.
[10]
Gershon. M. E., Mine Scheduling Optimization with Mixed Integer Programming,
AlME Fall Meeting, Honolulu, Preprint No. 82- 324, 1982.
[11]
Kim, Y. C., Knudsen, H. P. and Baafi, E, Y., Development of Emission Control
Strategies Using Conditionally Simulated Coal Deposits, University of Arizona,
Tucson, Proprietary report prepared for the Homer City Owners, Homer City, Pa.
15478, 1981.
[12]
Padberg, M W, Linear optimization and extensions, Springer, NY, 1995.
[13]
De Wet N., Homogenizing/Blending in South Africa - An update, Bulk solids
handling, Issue no.1, 1994.
[14]
Bivand, R., Pebesma, E., Rubio, V., Applied Spatial Data Analysis with R. Use R
Series, Springer, Heidelberg, 2008.
[15]
Murphy, T.D., Brown, K.E., Combining geostatistics and simulation to predict
sulphur at a central Illinois coal mine, Mining
Engineering (1993), 45, 284287.
[16]
Rossiter, D. G., Introduction to the R Project for Statistical Computing for
use at ITC, 3rd Edition. International
Institute for 15 Geo-information Science & Earth Observation (ITC),
Enschede, Netherlands, 2009.